how to find null space
Part 11 : Row Space, Column Space, and Null Space
![]()
Row Space
The span of row vectors of any matrix, represented as a vector space is called row space of that matrix.
or
If we represent individual columns of a row as a vector, then the vector space formed by set of linear combination of all those vectors will be called row space of that matrix.
Assuming a 3x3 matrix A
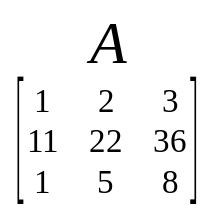
Dividing matrix A into row vectors we get
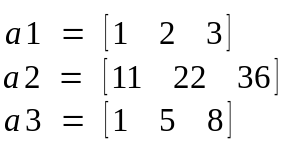
Row space of matrix A will be
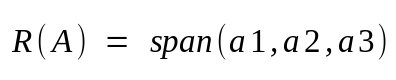
Column Space
Similar to row space, column space is a vector space formed by set of linear combination of all column vectors of the matrix.
Column vectors of matrix A
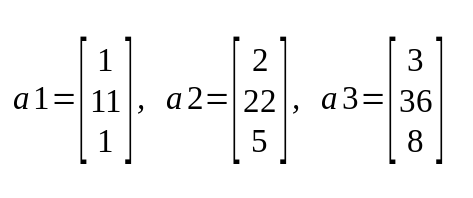
Column space of matrix A will be
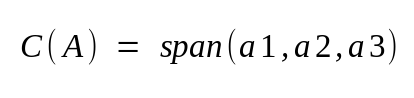
Both of these spaces have same dimension (same number of independent vectors) and that dimension is equal to rank of matrix. Why?
Because, rank of matrix is maximum number of linearly independent vectors in rows or columns and dimension is maximum number of linearly independent vectors in a vector space (like column space or row space).
Rows and columns of a matrix have same rank so the have same dimension.
Null Space
We are familiar with matrix representation of system of linear equations.
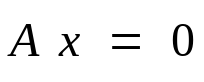
We can also find it's solution (values of variables for which the equation above is satisfied) using Gaussian Elimination algorithm.
If we take a set of all possible solution vectors (all possible values of "x"), then the vector space formed out of that set will be called null space.
Or
Null space contains all possible solutions of a given system of linear equations.
Taking an example
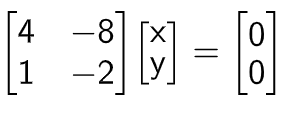
Solution vector of system of linear equations above is
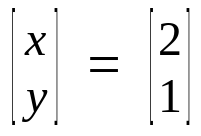
So this system of linear equations has two vectors in null space.
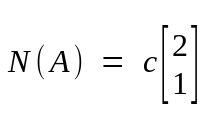
Null space always contains zero vector.
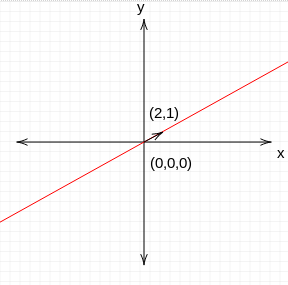
Nullity
Dimension of null space is called nullity.
Nullity of the system above is 1.
how to find null space
Source: https://medium.com/linear-algebra/part-11-row-space-column-space-and-null-space-d69319f22fc4
Posted by: ramirezcating1942.blogspot.com

0 Response to "how to find null space"
Post a Comment